RESONERA MERA!

Svenska fioler med resonanssträngar

Den resonanssträngsfiol som jag har byggt har en klang som är ganska fiollik och inte så mjuk i tonen som andra resonanssträngsfioler (eller hardingfelor). Jag har tolkat detta som att det beror på att halsvinkeln är mer lik fiolens än de traditionella resonanssträngsfiolernas. Jag hade planerat att bygga en fiol med samma halsvinkel som "Bulan" men förändrade detta under projektets gång eftersom den greppbräda jag gjorde blev ganska tunn och ledde till en väldigt låg stallhöjd. Eftersom "Bulan" bara är en hals är det svårt att uttala sig om stallhöjd och greppbräda.

Joseph Curtin hävdar till skillnad från min magkänsla att stalltrycket inte spelar så stor roll och det är möjligt att han har rätt.

Jag har börjat filosofera lite vad halsvinkeln egentligen är. Sarnell & Dagnell definierar den som den vinkel halsen måste monteras för att en linje som förlängs i greppbrädans riktning ska bli 28 mm vid stallet. I byggbeskrivningar för en vanlig fiol är halsens höjd över locket konstant och strängarnas höjd över greppbrädan likaså. För resonanssträngade fioler är normerna inte lika fasta och det går att variera flera parametrar. Till exempel kan halsen sticka upp längre än 5 mm över locket, stallet behöver inte göras med samma höjd som en vanlig fiol och vinklarna kan ändras efter eget tycke. Jag har därför funderat på vad det egentligen är som avgör trycket som strängarna utövar på stallet. Googling visade att det inte bara är jag som har funderat över dettta utan många har ställt upp ekvationer för de statiska krafter som verkar på en uppsträngad fiol.

I denna vy som visar en fiol från sidan har jag ritat ut krafterna som strängdraget bidrar med. Den del av strängdraget som verkar på stallet erhålls genom F * cosinus (vinkeln mellan stallet och strängarna). Stalltrycket är summan av krafterna i riktning mot översadeln och krafterna i riktning mot nedersadeln.

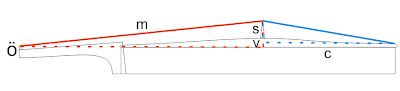
Om man ritar ut två trianglar mellan stallet, den plana linje som går längs sargens ovansida (denna är i och för sig inte alltid vinkelrät mot stallet eftersom sargen ibland görs lägre i framkant men vi approximerar här att den är rät) och nedersadeln/översadeln kan vi med genom några enkla mått räkna fram strängvinklarna. För den främre triangeln är stallhöjden (s), lockets välvningshöjd (l), översadelns avtånd upp till den plana linje som löper längs sargen ovansida (ö) samt mensuren (m) intressanta. För den bakre triangeln är det stallhöjden, välvningshöjden och halva corpuslängden (c) som vi kan använda. Krafterna på stallet blir då:

Det finns också formler för att beräkna frekvensen (f) för en sträng utifrån strängens densitet (d), längd (mensuren m) och hur spänd den är (S). Den ser ut så här:

Om vi bollar med ekvationen för att få fram strängspänningen S blir den

Om vi bestämmer oss för att inte variera vilken typ av sträng vi använder och stämmer fiolen normalt kan vi skriva om ekvationen för att få fram strängspänningen med en konstant som ersätter densiteten och frekvensen. Hur stor den är spelar inte så stor roll om vi ska jämföra olika stalltryck där dessa storheter är lika.

Om vi ersätter F i ekvationen ovan med S enligt denna formel får vi stalltrycket T som

s,v,ö,c och m är ganska enkla mått att ta och vi kan därför räkna ut stalltrycket och jämföra detta med en standardfiol. Jag har räknat med följande värden för en standardfiol:

Om vi jobbar med fioler som har en normalstor corpuslängd kan vi enkelt fixa ett diagram som visar stalltrycket som funktion av avståndet mellan översadel och stallets topp i höjdled samt mensurlängden. Det ser då ut så här (z-axeln är stalltryck i % av en normalfiols, x-axeln är mensurlängd och y-axeln är stallhöjden kompenserat för översadelns position i förhållande till sargen).

Om man analyserar hur stalltrycket förändras med ändrad mensur och stallhöjd kan man konstatera att en förändring av mensuren med X% alltid kommer att påverka trycket mer än motsvarande förändring av stallhöjden. Däremot påverkar det så klart mer att ändra stallhöjden en millimeter än mensuren en millimeter eftersom det blir en större procentuell förändring.

Copyright 2009-2020 Jon Magnusson